Odin, god of wisdom.

This is the second in my series of articles about Knowledge and Common Knowledge in a Distributed Environment, a beautiful and difficult 1990 paper about distributed systems and epistemology. So far, I analyzed the “muddy children puzzle,” I defined levels of knowledge, and I used these levels of knowledge to analyzed the Raft protocol (which was published long after this paper).

Now, the moment you’ve been waiting for: coordinated attack!

Coordinated attack #

Chinese general Guan Yu.

Two generals are encamped on hilltops, on either side of the enemy army. If they attack simultaneously, they’ll win, otherwise they’ll fail. They have no initial plan, so they send messengers back and forth, to try to agree on a time to attack. Unfortunately, messengers can be unpredictably slow, or they can be caught by the enemy. How can the generals agree on a time?

(The paper’s authors, Halpern and Moses, call this problem “coordinated attack” and they say it was introduced by Jim Gray in 1978. The puzzle may be older than that. Sometimes it’s called “Chinese generals.” The “Byzantine generals problem” is a more complex version that Lamport described later.)

As you probably know, the generals can never agree. If general A sends a message saying, “attack at dawn,” he doesn’t know whether B received it, so he risks attacking alone. So perhaps the protocol is, “attack if you proposed a time and received acknowledgment”? But if B receives and acknowledges the message, she doesn’t know whether A got her acknowledgment, so she also risks attacking alone. And so on. No protocol in this asynchronous system can guarantee they attack simultaneously.

Halpern and Moses (citing earlier work) use a many scenarios argument to prove that coordinated attack is impossible. If A sent the message and hasn’t observed an acknowledgment, there are many scenarios that fit his observations:

• The message was lost
• The message is still in transit
• The message was received and the acknowledgment was lost
• The message was received and the acknowledgment is still in transit

General A’s knowledge is the set of facts that are true in all the possible scenarios that match his observations.

So A knows his message was sent, but that’s it. If B receives the message and sends an acknowledgment, she also has four scenarios she can’t distinguish. The generals can’t be sure they’ve agreed to attack unless A knows that B knows that … infinitely. In other words, their attack time must be common knowledge, and common knowledge is impossible in an asynchronous system.

(Yes, this is related to FLP impossibility.)

Definition of knowledge #

Here’s my favorite part of the paper. It begins with a mathematical model of a distributed system, which will be familiar to people who use PlusCal, TLA+, or other formalizations. There are some processors (aka nodes or agents) called p₁, p₂, …, p_n. A run of the system is just like a TLA+ behavior: a sequence of events starting at time 0 and continuing infinitely (perhaps reaching a final state and staying there forever). The system is characterized by the set of all possible runs, R. This is just like a TLA+ state graph. A point (r, t) is a moment in a run r at time t. At every point, each processor has its own local history, the events it has observed, including its own actions. E.g., a Raft node knows the actions it’s taken and the messages it’s received, but it has no direct knowledge of other nodes’ histories. A protocol is a function of a processor’s local history: each processor deterministically chooses its next action based on its observations so far.

A processor p_i knows a fact $\varphi$ at point (r, t) if $\varphi$ is true at all points of R that are indistinguishable from (r, t). By indistinguishable points, I mean all points (r', t') where p_i’s local history is the same as at (r, t). For example, if I observed my partner Jennifer go out the front door, and I haven’t seen her come back in, then I know she’s gone, based on my local history of observations. She might have taken the car or gone for a walk—since I haven’t looked in the parking lot, those two scenarios are indistinguishable to me. But “Jennifer’s gone” is true in both scenarios, so I know that fact.

In Raft, if the leader has sent a log entry to both followers and only one follower has acknowledged it, then the leader can’t distinguish between the scenarios where one or two followers received the entry. But “the entry is majority-replicated” is true in both scenarios, so the leader knows that fact.

A processor’s view of the system is a function of its history. The view could just be the identity function—the processor’s view is its history, i.e. the sequence of all its actions and observations. Or the processor’s view could be a summary of its history, e.g. the Raft election protocol requires a node to remember only the most recent vote it cast, not the sequence of all its past votes. In TLA+ we usually have some variables for each node, which are updated when nodes take actions or receive messages: these are the nodes’ views, their summaries of their local histories!

Halpern and Moses more formally define a processor’s view of the system, and how that relates to levels of knowledge, like distributed knowledge and common knowledge, in Section 6 of the paper. It’s great, go read it.

Indistinguishability graph #

As a TLA+ guy, I usually think of a state as an assignment of values to variables, and the state graph connects states with directed edges representing possible state transitions. Let’s consider the muddy children from the previous episode. Say there are two children. Our variables are:

• a, b: Whether child a and/or b is muddy.
• m: Whether the father has announced, “At least one of you is muddy.”
• q: The number of times the father has asked, “Can you prove you’re muddy?”

The initial state is:

$a \in \{\text{true}, \text{false}\} \land b \in \{\text{true}, \text{false}\} \land m = \text{false} \land q = 0$

Then the father makes his announcement (m becomes true), and then he starts asking his question (q increases). We know at least one child is muddy; let’s say that’s child a and the maybe-muddy one is b. Here are the states and transitions:

How can we use this graph to represent what the children know? For any two states, let’s add a non-directed edge between them if some child has the same view in both states, i.e. the states are indistinguishable to that child. And let’s label the edge with the name of the child who can’t distinguish the states:

Child b can’t distinguish if it’s muddy or clean in the initial state, so there’s a blue “b” edge between the first two initial states. The two states are distinct in a’s eyes, because it can see whether b is muddy, so we don’t label the edge “a”. After the father announces “at least one of you is muddy,” b still doesn’t know if it’s muddy, because it sees that a is muddy so a might be the only muddy child. Therefore the two next states are also indistinguishable to b. Finally the father asks, “can you prove you’re muddy?” As I explained in the previous article, a and b now know if they’re muddy, so the third states are distinct to both of them and there’s no blue edge.

Can we do the same for Raft? The real Raft TLA+ spec has dozens of variables. Let’s simplify. Let’s say there’s one log entry, there’s a permanent leader, and there are two followers f₁ and f₂. Here are our variables:

• r₁, r₂: Follower f₁ or f₂ has received the entry (“r” for “receive”).
• a₁, a₂: The leader received an acknowledgment from f₁ or f₂ (“a” for “acknowledge”).

At first all the variables are false. Then f₁ or f₂ receives the log entry, and some sequence of receiving and acknowledging leads to the final state, where both followers have received and acknowledged the entry. Here’s a state-transition graph, false is white and true is red:

In the last article I defined two facts:

• $\varphi$ (phi): the log entry exists
• $\psi$ (psi): the log entry is majority-replicated

A follower knows $\varphi$ if it received the entry, and the leader knows $\psi$ if it knows at least one follower knows $\varphi$, since the leader plus one follower is a majority of the three-node replica set. In other words:

$$K_{leader} \psi \Longleftarrow K_{leader} S_F \varphi$$

Let’s analyze this with the graph. A follower f knows $\varphi$, if $\varphi$ is true in all the states indistinguishable to f from this state. The only variable in f₁’s view is r₁, so all states with the same r₁ value are indistinguishable to f₁. For f₁’s indistinguishability graph, I’ll draw edges between the nodes where r₁ is true, and edges between the nodes where r₁ is false:

The graph for f₂ is the same, but flipped vertically.

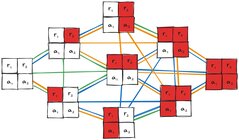
The leader doesn’t know whether a follower has received the entry, so states that differ only by their r₁ or r₂ values are indistinguishable to the leader. The leader knows what acknowledgments it received, so it can distinguish states by their a₁ or a₂ values.

Putting it all together:

As I said earlier, “the leader knows $\psi$” is equivalent to “the leader knows that at least one follower knows $\varphi$.” We can evaluate a property like this with the indistinguishability graph. The leader knows f₁ knows $\varphi$ at a state S, if every path from S along zero or one leader edges, then zero or one f₁ edges, leads to a state where f₁ knows $\varphi$:

This is a graph-style way of saying:

• the leader knows f₁ knows $\varphi$ in state S, if
• in all states T indistinguishable (to the leader) from S,
• f₁ knows $\varphi$ in all states indistinguishable (to f₁) from T !

The same goes for states where the leader knows f₂ knows $\varphi$:

Putting it all together:

As you’d expect, the leader knows $\psi$ in states where a₁ or a₂ is true; i.e. states where one or the other follower has acknowledged the entry. But it’s cool to see how it can be expressed as a graph query. This seems ripe for automatic verification. Halpern and Moses describe how various levels of knowledge, such as distributed knowledge, or “everyone knows,” or “everyone knows that everyone knows,” are properties of paths through the indistinguishability graph.

I’ll stop here and let my brain cool off. Next time: agents in a distributed system can achieve common knowledge if they have reasonably reliable clocks.

Odin and other Norse images by Gerhard Munthe.