Athena, goddess of wisdom.

This is the third in my series of articles about Knowledge and Common Knowledge in a Distributed Environment, a 1990 paper by Joseph Halpern and Yoram Moses. I’ve defined knowledge and levels of knowledge, and used this framework to analyze the muddy children puzzle and the Raft protocol. I got excited about the connection of knowledge to graph theory, so I took a self-guided detour, applying graph theory to knowledge in Raft. Now we’ll return to the actual paper, with the authors’ proof that “coordinated attack” is impossible in an asynchronous system, but possible in a synchronous one.

Coordinated attack in an asynchronous system #

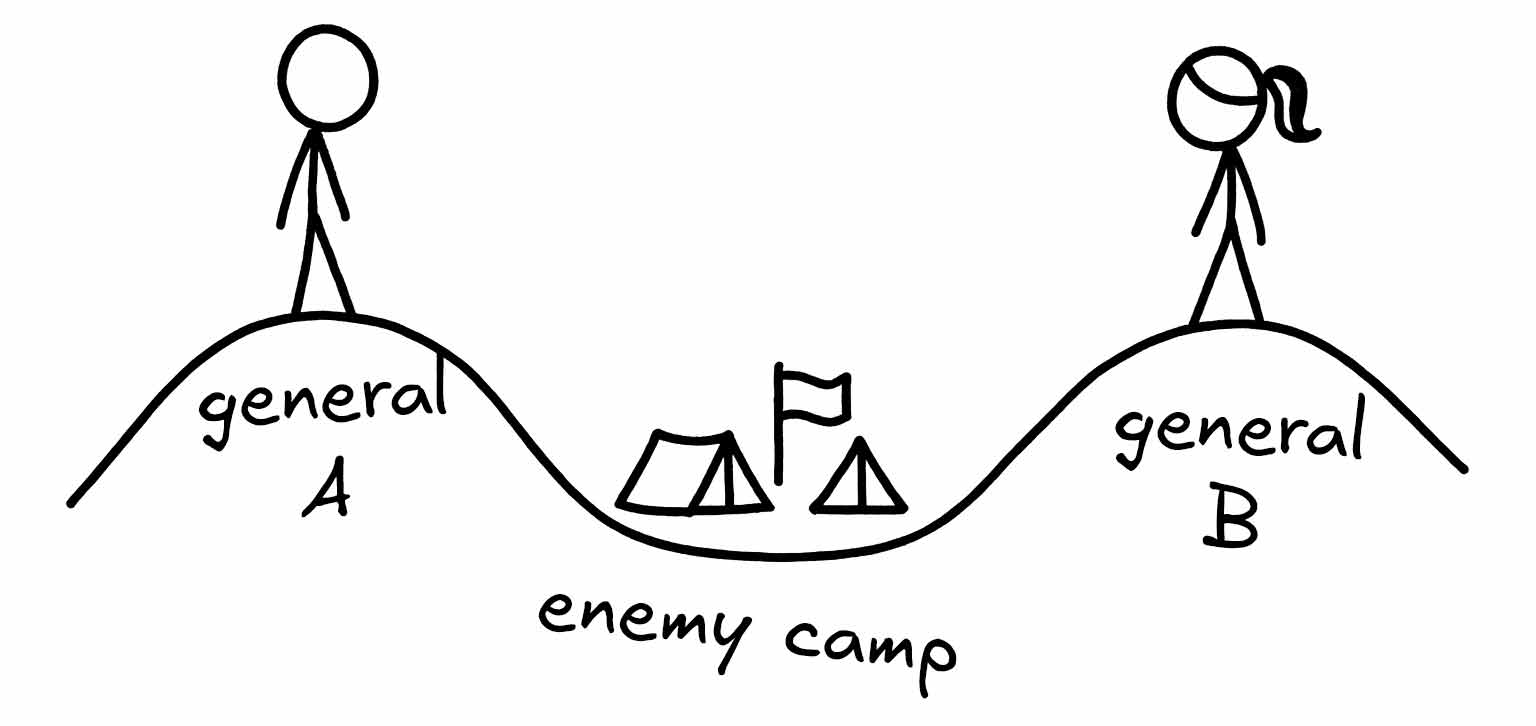
We saw the coordinated attack problem in the last article. Two generals named A and B try to decide when to attack their common enemy, but their messages can be delayed indefinitely, or lost. We assume the generals are following correct protocols (they won’t attack alone) and that they’re deterministic: a general always makes the same decision given the same history (all its observations so far). Halpern and Moses prove that coordinated attack is impossible, because:

If both generals are attacking,
then they must both know they are both attacking,
and this must be common knowledge,
but common knowledge can’t be achieved in an asynchronous system.

Let’s walk through their proof. Throughout, $\psi$ (the Greek letter psi) is the fact “both generals are attacking.”

Lemma 1: “If both generals are attacking, then everyone knows they are both attacking.” Or in formal notation:

\psi \Rightarrow E \psi

Proof: Let’s say that A attacks at some point (r, t), which is a possible moment in a run r at time t in the system. Recall the definition of knowledge: A knows the fact $\psi$ if $\psi$ is true in all scenarios that match A’s observations so far; i.e., all the points where A would have the same history as it has at point (r, t). Since A’s protocol is deterministic, A must attack in all these scenarios, and since A’s protocol is correct, B must also attack in all these scenarios. Therefore A knows $\psi$ . We can switch the names A and B to prove B also knows $\psi$ , thus everyone knows $\psi$ .

Lemma 2: “If both generals are attacking, it’s common knowledge that both are attacking,” i.e.:

\psi \Rightarrow C \psi

The authors assert this based on “the induction rule,” on page 15 of the paper:

\text{If } \varphi \Rightarrow E ( \varphi \land \psi ) , \text{then } \varphi \Rightarrow C \psi

For example, in the muddy children puzzle, $\varphi$ is the father’s announcement that at least one child is muddy, and $\psi$ is the fact that at least one child is muddy. In Coordinated Attack, $\varphi=\psi$ , i.e., “both generals are attacking,” which makes the induction rule:

\text{If } \psi \Rightarrow E \psi , \text{then } \psi \Rightarrow C \psi

They don’t prove the induction rule, but I think I see how to do it.

Assume that $\psi \Rightarrow E^k\psi$ . That is, $\psi$ implies that everyone knows that everyone knows that everyone knows … $\psi$ , where “everyone knows” is repeated k times.
Well, if $\psi$ is true and I’m one of the agents in the system, I know $\psi$ and I know its implication. Thus I know $E^k\psi$ , and so does everyone else.
Therefore $E^{k+1}\psi$ .
We can repeat this inductive step infinitely, therefore $C\psi$ .

Lemma 3: If achieving $C\psi$ requires message-passing, then achieving it is impossible in an asynchronous environment where any message can be delayed indefinitely or lost.

Halpern and Moses’s proof of this is baffling, with a dozen variables, some of which seem to be reused with different meanings in the same paragraph. Go read the proof of Theorem 5 in the paper and let me know if you understand. Here, instead, is my intuition about why common knowledge can’t be attained.

First, to achieve $C\psi$ , all agents must simultaneously learn $C\psi$ : by definition, it’s impossible for some agents to know $C\psi$ and others not to know, so they must all learn at once.
Second, we said that learning $C\psi$ requires message-passing, so there must be some message m that they all receive simultaneously, from which they learn $C\psi$ .
But this is an asynchronous environment, so if agent A receives m, it can’t at that moment know whether B has. The scenario where B learns $C\psi$ is indistinguishable to A from the case where it doesn’t. This is a contradiction, so $C\psi$ can’t be achieved in an asynchronous world.

(You can generalize to multiple messages. That is, A must receive a message $m_a$ at the same moment B receives $m_b$ to achieve $C\psi$ . The same argument holds.)

If $C\psi$ doesn’t require message-passing, then it can be achieved. For example, there might be a thunderstorm that A knows B must have noticed, and vice versa, so common knowledge of the thunderstorm is attainable. Or, if the agents have synchronized clocks, then at noon it’s common knowledge that it’s noon. But these exceptions don’t help our generals, who didn’t have the foresight to make a plan like, “attack during the next thunderstorm,” or “attack at noon.” So they’re hosed.

Disappointingly, the only correct protocol for coordinated attack in an asynchronous environment is: “Never attack.”

What if message delay is bounded? #

So we proved common knowledge is unachievable by passing messages if their delay is unbounded. What if it’s bounded: what if message delivery is guaranteed with a maximum delay of $\epsilon$ (Greek letter epsilon), and this maximum is common knowledge?

Let’s say both generals have reliable timers, but not necessarily synchronized clocks. General A sends a message m like “let’s attack at noon tomorrow,” and $\epsilon$ is much shorter than the time between now and noon tomorrow. The messenger leaves General A’s camp at start time $t_S$ , a time known only to General A. Obviously, A immediately knows he sent m:

now ≥ t_S \iff K_A sent(m)

But A doesn’t know how much delay his message will have. Once the current time is $t_S + \epsilon$ , he knows his message has been delivered, so he knows B knows he sent it:

now ≥ t_S + \epsilon \iff K_A K_B sent(m)

General B receives the message at delivery time $t_D$ , a time known only to her. She doesn’t know how long m was delayed, so she doesn’t know $t_S$ , so she doesn’t know when A will know she got m. In the worst case, the delay was $\epsilon$ but she worries it was zero, so she waits until $t_D + \epsilon$ , which is $t_s + 2 \epsilon$ . General A can thus reason that B knows A knows B got m after a $2 \epsilon$ delay. In other words:

now ≥ t_S + 2 \epsilon \iff (K_A K_B)^2 sent(m)

But General B isn’t sure the current time is at least $t_S + 2 \epsilon$ until (in the worst case) it’s actually $t_S + 3 \epsilon$ , so she has to wait another epsilon before she knows $(K_A K_B)^2 sent(m)$ . General A knows all this about General B, so now $(K_A K_B)^3 sent(m)$ is true. We can infer that for $k \gt 0$ :

now ≥ t_S + k \epsilon \iff (K_A K_B)^k sent(m)

We proved earlier that the generals can’t attack together unless their plan is common knowledge, which means $(K_A K_B)^\infty\ sent(m)$ , but that would take infinitely long. So not even guaranteed message delivery with bounded delay is enough to solve coordinated attack.

Another indistinguishability graph #

Let’s look at this from another angle, with the indistinguishability graph technique from the previous article.

Here’s a state graph, with timestamps in blue going down the left side. The black arrows are possible state transitions. In the initial state, m is unsent. In the next state, General A sends it. Then there’s a branch: m is received after zero delay or $\epsilon$ delay. Then the two branches continue separately, making a state transition after each $\epsilon$ of time passes. The first two states are connected with a green line because they’re indistinguishable to General B: she doesn’t know if A sent the message or not. After that, there are two possible states at each timestamp, and these two states are connected with red lines because they’re indistinguishable to General A: he doesn’t know if his message was received after zero delay or $\epsilon$ delay. The diagonal green lines indicate the same thing about General B: she doesn’t know if she received the message after a delay or not. (My drawing is a hybrid of a state graph and a Kripke structure.)

Like we saw in the last article, we can use properties of this graph to calculate agents’ knowledge. For example, $K_A K_B sent(m)$ is true in state s iff all paths from s that follow zero or one A-indistinguishable edges, then zero or one B-indistinguishable edges, end at a state where $sent(m)$ is true.

Let’s choose a particular state as a demonstration: the state where the current time is $t_S$ and B received m with zero delay. We can follow one A-edge, then zero B-edges, and arrive at the state labeled “sent”, where $sent(m)$ is true. Or we can follow the same one A-edge, and then one B-edge and arrive at the state labeled “unsent,” where $sent(m)$ is false. Since both “sent” and “unsent” are reachable from the current state, $K_A K_B sent(m)$ is false.

$K_A K_B sent(m)$ is false in the state marked “current state.”

But if you start from either of the states where the current time is $t_S + \epsilon$ and follow zero or one red edges, then zero or one green edges, you always arrive at states where m was sent. Thus $K_A K_B sent(m)$ is true in those states.

$K_A K_B sent(m)$ is true in the state marked “current state.”

But if you want a state where $(K_A K_B)^2 sent(m)$ , you need to start farther away, at one of the states where the time is $t_S + 2 \epsilon$ or later. Otherwise there exists a path that follows a red, then green, then red, then green edge and arrives at a state where $sent(m)$ is false. (I haven’t drawn a picture of this.) Continuing inductively, we can see how the graph expresses the same thing we proved before: $(K_A K_B)^k sent(m)$ is true only if the current time is $t_S + k \epsilon$ or later.

What if the generals have synchronized clocks? #

It seems weird to conclude that the generals can’t coordinate, even with bounded message delays. Isn’t it enough for A to say, “attack at noon tomorrow” at least $\epsilon$ before that time, with no acknowledgment from B? Yes, this works, but the protocol itself must be common knowledge at the start, and the generals must have perfectly synchronized clocks. If the generals have already agreed that A will send a message proposing an attack at least $\epsilon$ in the future, then when B receives “attack at noon tomorrow,” she knows:

General A sent this at least $\epsilon$ before noon (that’s the protocol)
Therefore at noon, A knows B received it
Therefore at noon, B knows A knows B received it
And so on…

At noon common knowledge is achieved, because both generals can reason about what the other knows will be true at the deadline.

Halpern and Moses don’t propose this exact idea. They instead use timestamped messages: “The time is now $t_S$ , let’s attack at noon.” This removes General B’s uncertainty about $t_S$ , so at time $t_S + \epsilon$ the plan becomes common knowledge. This is pretty much equivalent: my pre-agreed protocol and their timestamped messages both provide extra shared facts from which the two generals can reason.

Both solutions require perfectly synchronized clocks. If A and B have the slightest uncertainty about when noon arrives, they can’t become sure of the plan simultaneously, so they can never achieve common knowledge.

Weaker forms of common knowledge #

This still seems weird. In practice, I can arrange to meet someone for lunch, and a Raft system can reach consensus, so why is it impossible in theory? It’s because Halpern and Moses’s definition of common knowledge is impractically strong. So they define weaker forms of shared knowledge that are achievable and suffice for consensus or lunch.

$\epsilon$ -common knowledge ( $C^{\,\epsilon}\phi$ ): Instead of $\phi$ becoming common knowledge simultaneously, $\phi$ becomes “ $\epsilon$ -common knowledge” in an $\epsilon$ time window. So if message delivery is guaranteed after some bounded delay, its contents are common knowledge a bounded time after it’s sent.

Timestamped common knowledge ( $C^T$ ): Everyone knows at time T on their own clock. If clocks are perfectly synchronized, then $C^T$ is equivalent to common knowledge. If they’re synchronized within $\epsilon$ , then $C^T$ is $C^{\,\epsilon}$ . You can discard clocks and substitute something like a Raft term number for the timestamp and say, “which node is the leader in term t is timestamped common knowledge.”

Eventual common knowledge ( $C^{\,\diamond}$ ): Everyone will eventually know, though not necessarily at the same time. This suffices for actions that must eventually happen everywhere, without a deadline.

These form a hierarchy: $C \Rightarrow C^{\,\epsilon} \Rightarrow C^{\,\diamond}$ .

Internal knowledge consistency #

Another solution to the paradox—common knowledge is impossible in theory but possible in practice—is “internal knowledge consistency.”

Every agent in the system has an interpretation of its observations. Formally, an interpretation is a function that takes the agent’s personal history and the current time, and outputs a set of facts the agent believes are true. For example, in the muddy children puzzle, after the children hear the father’s announcement m, “at least one of you is muddy,” each child believes it heard m. An interpretation is “knowledge consistent” if it produces only true beliefs.

A knowledge consistent interpretation must say that m isn’t common knowledge, because in reality, the children can’t achieve common knowledge of m: How do they all know that they all understand English, and they were all paying attention, etc.? But an internally knowledge consistent interpretation can say it is, so long as no observation will ever contradict this belief. This matches how we intuitively reason about knowledge and common knowledge in everyday situations.

This concludes my review of Halpern and Moses’s “Knowledge and Common Knowledge in a Distributed Environment”! But I’ll have more to say about epistemic logic and distributed systems. I’m now in a UCLA seminar with Remy Wang, reading Reasoning About Knowledge, the short book Halpern and Moses wrote with Ronald Fagin and Moshe Vardi. My goal now is to marry epistemic logic with TLA+, by analyzing a TLA+ specification’s state graph.

Images:

A. Jesse Jiryu Davis